理解卷积
卷积的内涵
先给公式,函数和函数的卷积:
什么意思呢?对于任意的输入信号,都可以表示为
即,任意输入信号均可分解为冲激函数的线性组合。输入信号为单位冲激函数(幅值为1)时,把对应的输出(响应结果)定义为。也就是说,是系统对单位冲激函数的响应。注意,这个响应函数是系统决定的,每个系统都有自己的函数,因此也叫系统函数:
如下图所示,如果系统的输入在时刻的幅值为,那么系统对它的响应就是。
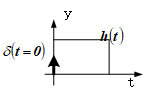
也就是说,该输入对应的系统输出为:
事实上,而实践中,输入一般是连续的信号。例如,在时刻,系统的输入为,则该输入相应的输出为。因此,如果在任一时刻,系统中的输入为,那么该输入对应的输出为。而时刻时的输出,不只是当前时刻的输入的作用,还包括之前的所有时刻的输入带来的作用。因此,系统在时刻的输出,是时刻之前所有时刻的输入信号作用的求和。即
写成积分的形式,即可得到式(1)。
因此,式(1)的含义是:系统时刻的输出,是该时刻之前的所有输入引起的响应累积作用的结果。
图解法求卷积
把换成,重写卷积公式:
已知和的表达式以及函数图像,怎么求得二者的卷积结果呢?
为了理解方便,设和都是方框函数,
如下图所示。考察公式(3),求,就是求时刻之前,所有时刻与乘积的和。
为了求与的乘积并积分,需要首先分别画出,关于的图像。的图像直接根据表达式可以画出,如下图紫色矩形框所示。关于的图像则需要对函数图像依次做反褶(沿做镜像),然后右移,并计算在不同下,两个函数曲线所围的面积(如果f(0)=2呢,就不是面积了。这里为了举例方便,设置了,应该是)。
当时,需要对反褶的图像左移,然后计算两个函数曲线所围的面积。
- 当时,相当于对反褶的图像左移,两曲线无重叠区域,因此;
- 当,相当于对反褶的图像左移,反褶的图像右侧与左侧刚好重叠。
- 当,相当于对反褶的图像左移,二者重叠区域变大。
- 当,相当于对反褶的图像右移,二者重叠区域进一步变大。
- 当,相当于对反褶的图像右移,二者重叠区域达到极大值。
- 当,相当于对反褶的图像右移,反褶的图像将整体包围,二者重叠区域保持极大值。
- 当,相当于对反褶的图像右移,反褶的图像左侧与左侧重叠。
- 当,相当于对反褶的图像右移,反褶的图像左侧进入图像中,二者重叠区域随的右移而减小。
- 当,相当于对反褶的图像右移,反褶的图像左侧与图像右侧重叠,二者重叠面积变为0。
- 当,相当于对反褶的图像右移,反褶的图像左侧与图像右侧分别且随着增大而渐行渐远,二者重叠面积保持为0。
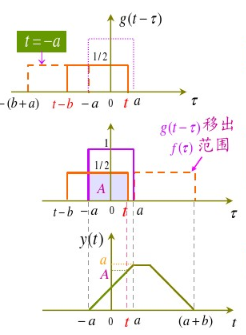
在此过程中,随着从逐渐增大到再到,反褶的图像其实从左侧无穷远处紧贴着逐渐向右滑动到反褶图像原本位置,再到右侧无穷远处。反褶的图像就像一个滑动的窗口,因此该方法也常称作滑窗法。
卷积的计算机算法
计算卷积的算法是"不进位乘法",如下图所示(计算机编程的算法,与上述图解法一样的):
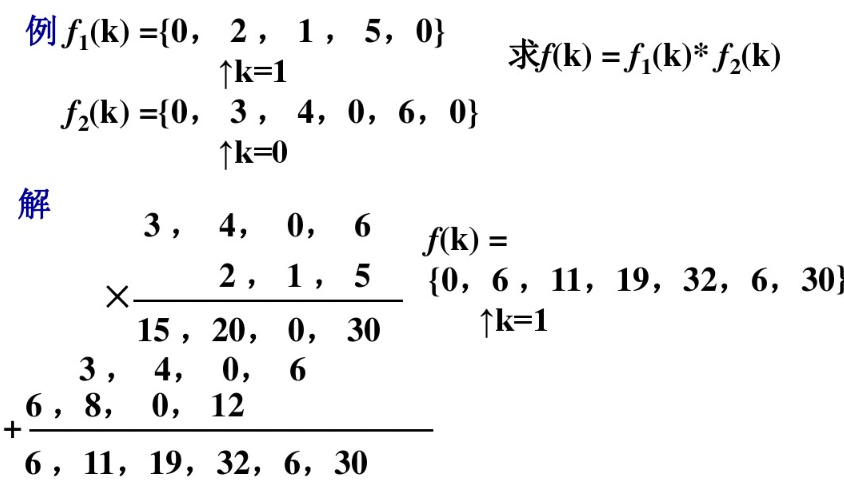
二维卷积
与一维卷积的滑窗类似,二维卷积也用滑窗进行计算。广泛用在图像处理领域。
以下内容转自CSDN博客
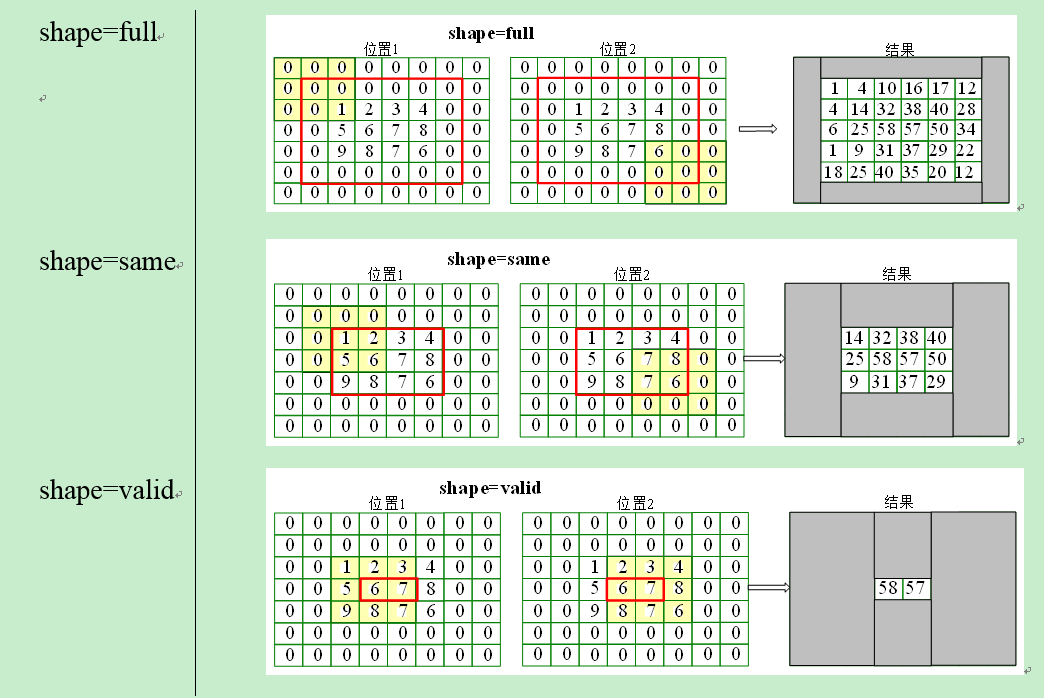
算法:对矩阵A,B进行卷积:conv2(A,B),其中A为图像矩阵,B为卷积核。
- 对矩阵A补零。如图。
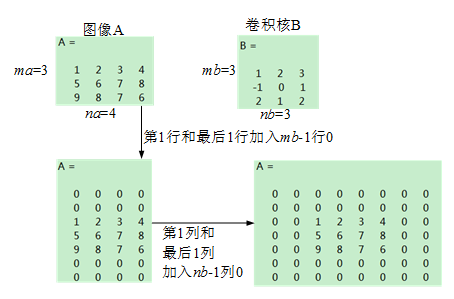
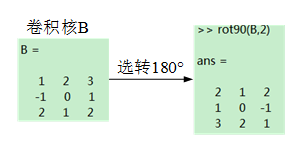
- 将卷积核B分别沿行方向和列方向进行反褶(相当于沿中心旋转180°)。如图。
- 滑动滑窗,将卷积核的中心位于图像矩阵的每个元素,求滑窗内两矩阵点积(按元素乘)之和。如图。
在图像处理中,卷积常用于对图像模糊处理,边缘检测,产生轧花效果等。
在深度学习中,卷积在卷积网络中发挥作用。