小波变换(二): 小波基函数,母小波和父小波

系列文章列表

本文是《小波变换》系列的第2篇，主要介绍为什么需要小波.

1. 小波变换(一): 为什么需要小波?
2. 小波变换(二): 小波基函数,母小波和父小波
3. 小波变换(三): 从实例代码看Haar小波分解和重构
4. 小波变换(四): 常用小波特点及二维小波变换
5. 小波变换(五): 小波，傅里叶与卷积的关系

小波级数展开与小波变换

上节我们给出了为啥需要小波变换，并给出了小波基函数，小波变换和小波级数的一般形式：

对于连续的信号，以$\varphi(\frac{t-\tau}{a})$为基函数的小波变换公式为： $$WT(a,\tau)=\frac{1}{\sqrt{a}}\int^{\infty}_{-\infty}{f(t)\varphi(\frac{t-\color{red}{\tau}}{\color{red}{a}})dt}\tag{1}$$

对于离散的信号，以$\varphi(2^{j}t-k)$为基函数，进行小波级数展开： $$f(t) = \sum_{k\in Z} c_{k}\varphi(2^{j}t-k),\text{here}\;c_{k}\in R\tag{2}$$

注意二者的小波基函数$\varphi(2^{j}t-k)$或者$\varphi(\frac{t-\tau}{a})$，本质是一样的。

• $a=2^{-j}$，以及$j$都起到缩放函数的作用，因此都是尺度因子，对应于傅里叶变换中的$\omega$的倒数(周期$T$)。
• $\tau=2^{-j}k$，以及$k$是平移因子。

已经了解了小波基函数的一般形式，那么其他各种网站，资料，论坛里说的母小波和父小波都是什么东西?

母小波的理解

下面以Haar小波为例，详细理解一下小波级数展开的过程，并介绍一下什么是母小波，什么是父小波。

以下是被好多好多人选择的小波：Haar小波。Haar函数(先记一下，其实Haar小波级数展开的母小波)为：

$$\varphi(t)= \begin{cases} 1 &0 \leq t < 1\\ 0 &\text{otherwise} \end{cases}\tag{3}$$

Haar函数在时域上不连续，性能一般，但胜在计算简单。

如果对其向右平移任意$k$个单位($k\in Z$)，构成一组函数$E=\{\varphi(t-k)\}$, 该组函数两两相互正交，易证明

$$\begin{aligned} \langle\varphi(t-k),\varphi(t-k)\rangle &=\int^{\infty}_{-\infty}\varphi^{2}(t-k)dt=1\\ \langle\varphi(t-k),\varphi(t-k')\rangle &\xlongequal[k,k'\in Z]{k\ne k'}\int^{\infty}_{-\infty}\varphi(t-k\varphi(t-k')dt=0 \end{aligned}$$

因此构成一组正交基，这组正交基的线性组合形成函数空间$V_0$。

此时如果将$\{\varphi(t-k)\}$的宽度缩小一半，同时保持缩放前后函数的总能量不变，则形成一组基函数$E=\{\sqrt{2}\varphi(2t-k)\}$，同样易证明这是另一组正交基,这组正交基的线性组合形成函数空间$V_1$。

不断缩小尺度，可形成一组基函数$E=\{\sqrt{2^{j}}\varphi(2^{j}t-k)\},s.t.\,j\in Z$,这组正交基的线性组合形成函数空间$V_j$。

在Haar小波变换中，所使用的基函数是$V_j$空间中的基函数(去除了$2^j$的系数)：

$$\varphi(2^{j}t-k)\tag{4}$$

$V_j$空间中的任意函数可以写作($c_j$中已经包含了$2^{j}$，此式等同于式(2))：

$$f_{j}(t) = \sum_{k} c_{k}\varphi(2^{j}t-k), \text{here}\;c_{k}\in R\tag{5}$$

现在，我们可以用这个阶梯状的函数去近似任意的原始的时域信号啦，不信你看！

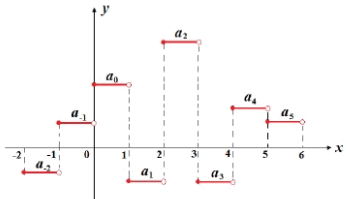
注意，我们现在从式(3)的$\varphi(t)$，经过一步步的缩放，平移形成了很多组基函数，这些基函数可以表达函数空间$V_{j}$的任意函数。再形象一些，空间$V_{j}$的任意函数都可以用变形过的$\varphi(t)$组合得到，因此，$\varphi(t)$就被定义为母小波。

好了，到这儿应该都没什么问题，那既然母小波已经完全可以表示$V_{j}$空间中的任意函数$f_{j}$，为啥还要搞出来一个父小波来pullze me? 接着往下看！

父小波的理解

在实际的信号处理实践中，使用公式(2)是比较难以操作的。例如，以下图的信号为例，高频的毛刺是我们不需要的，要滤除的。

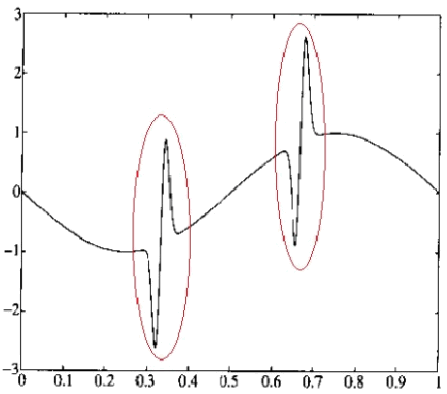
haar小波基函数的$j$越大，信号宽度越小，越接近噪声成分。因此，为了滤除噪声，需要很高的时间分辨率。但在低频部分，需要不太高的时间分辨率，$j$要小一些。

因此我们需要一种属于$V_j$但不属于$V_{j-1}$的尖峰函数，以匹配原始时域信号中的毛刺。

通过观察得到，函数空间$V_0$的任意基函数$\varphi(t-k)$可以被空间$V_1$中的基函数线性组合得到(如下图(a))，因此$V_0$是$V_1$的子空间。以此类推，容易得到

$$\varphi(2^{j}t)+\varphi(2^{j}t-1)=\varphi(2^{j-1}t)\tag{6}$$

于是$V_{j-1}$也是$V_{j}$的子空间。那么就有$V_0\subseteq V_1\subseteq\cdots\subseteq V_j$。

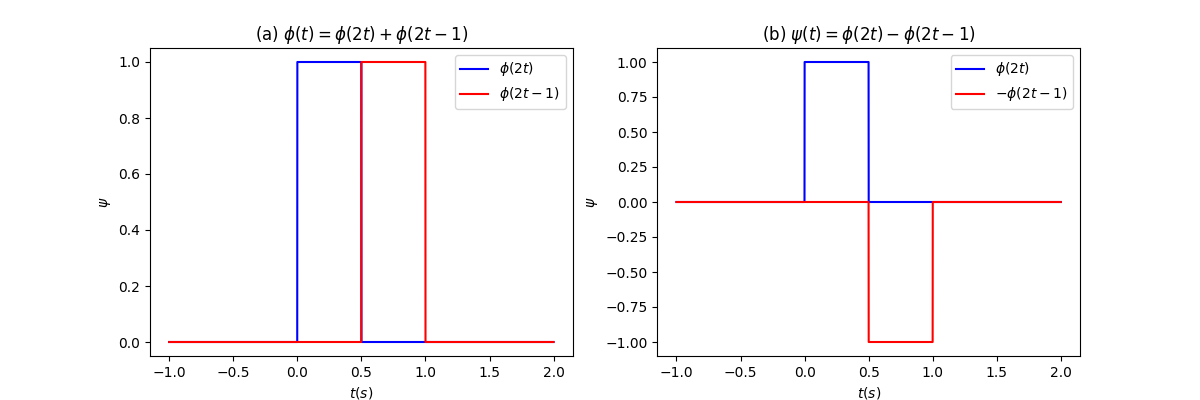
如果定义如上图(b)所示的$\psi(t)$，则$\psi(t)$是$V_{1}$空间中的一个函数：

$$\psi(t)=\varphi(2t)-\varphi(2t-1)\tag{7}$$

容易发现，对于$V_{0}$空间的任意的基函数$\varphi(t-k)$，都有$\langle \varphi(t-k),\psi(t)\rangle=0$。事实上，对$\psi(t)$平移$k$个单位后得到的函数$\psi(t-k)=\varphi[2(t-k)]-\varphi[2(t-k)-1]$，都与$V_{0}$空间正交。函数$\psi(t-k)$的线性组合也都与$V_{0}$空间正交。

进一步地，$V_{j}$空间中的函数

$$\psi[2^{j-1}(t-k)] = \varphi[2^{j}(t-k)]-\varphi[2^{j}(t-k)-1]\tag{8}$$

与$V_{j-1}$空间的所有函数均正交。以公式(8)中函数的线性组合，形成的空间$W_{j}$，是$V_{j}$的子集。

当$j$很大时，空间$W_{j}$表示的尖峰就与信号中的噪声十分相似了，为了滤掉噪声，可以把$W_{j}$中的项设为0。

接下来证明$V_{j}$空间是$V_{j-1}$空间与$W_{j-1}$空间的直和(如果$V_{j}$中的元素不属于$V_{j-1}$，就一定属于$W_{j-1}$)。

令式(8)中$k=0$，并联立式(6)，容易得到

$$\begin{aligned} \varphi(2^{j}t)&=\frac{1}{2}\left( \psi(2^{j-1}t)+ \varphi(2^{j-1}t) \right)\\ \varphi(2^{j}t-1)&=\frac{1}{2}\left( \psi(2^{j-1}t)- \varphi(2^{j-1}t) \right) \end{aligned}$$

因此有

$$\begin{aligned} f_{j}(t)&=\sum_{k \in Z} c_{k}\varphi(2^{j}t-k)\\ &=\begin{matrix}\underbrace{\sum_{k \in Z}c_{2k}\varphi[2^{j}(t-k)]}\\\text{even}\end{matrix}+\begin{matrix}\underbrace{\sum_{k \in Z}c_{2k+1}\varphi[2^{j}(t-k)-1]}\\\text{odd}\end{matrix}\\ &=\frac{1}{2}\left\lbrace\sum_{k \in Z}c_{2k} \left[ \psi(2^{j-1}(t-k))+ \varphi(2^{j-1}(t-k)) \right] \right.\\ &\quad\quad +\left.\sum_{k \in Z}c_{2k+1}\left[ \psi(2^{j-1}(t-k))- \varphi(2^{j-1}(t-k)) \right]\right\rbrace\\ &=\left\lbrace\sum_{k \in Z}\frac{c_{2k}+c_{2k+1}}{2} \left[ \psi(2^{j-1}(t-k))\right] \right.\\ &\quad +\left.\sum_{k \in Z}\frac{c_{2k}-c_{2k+1}}{2}\left[ \varphi(2^{j-1}(t-k)) \right]\right\rbrace\\ &=w_{j-1}+f_{j-1} \end{aligned}$$

因此，容易得到

$$f_{j}(t)=w_{j-1}+f_{j-1}=w_{j-1}+w_{j-2}+w_{j-3}+\cdots+w_{0}+f_{0}\tag{9}$$

这表示$V_{j}$中的任意函数，可以写作$W_{j}$中的函数和$V_{j-1}$中函数的线性组合。因此$W_{j-1}$是$V_{j-1}$的正交补：$W_{j-1}$与$V_{j-1}$相互正交，且互为补集。

$$\begin{aligned} V_{j}&=W_{j-1}\bigoplus V_{j-1}\\ &=W_{j-1} \bigoplus W_{j-2} \bigoplus V_{j-2}\\ &=W_{j-1} \bigoplus W_{j-2} \bigoplus \cdots \bigoplus W_{0} \bigoplus V_{0} \end{aligned}\tag{10}$$

公式(10)意思就是：如果使用公式(2)进行信号近似，本质上是使用$\varphi(t)$和不同尺度的$\psi(t)$进行近似，也就是使用阶梯和毛刺近似了任意信号$f(t)$。根据公式(9)，有

$$\begin{aligned} f(t) &\approx f_{j}(t)\\ &=\left\lbrace w_{j-1}+w_{j-2}+\cdots+w_{0}+f_{0}\right\rbrace\\ &=\sum_{j=1}^{\infty}\sum_{k\in Z}c_{j,k}\psi[2^{j-1}(t-k)] + \sum_{k\in Z}d_{k}\varphi(t-k) \end{aligned}\tag{11}$$

看到了吗，任意一个函数$f(t)$，可以用$\psi$经过一系列缩放、平移形成的函数，和$\varphi(t)$经过平移形成的函数的线性组合来表达。

也就是说，这里我们只把母小波进行平移，把父小波进行缩放、平移，组合可以得到任意函数。

相信你已经理解父小波为什么还叫做尺度函数(scaling function)了吧！

为了强化记忆，我们把公式(11)抄写一遍：

$$f(t) =\sum_{j\in N}\sum_{k\in Z}c_{j,k}\psi[2^{j}(t-k)] + \sum_{k\in Z}d_{k}\varphi(t-k)\tag{12}$$

事实上，在实践过程中，我们用的更多的是公式(12)而不是公式(2)。首先将信号转换为小波分量，要滤除$j$对应的毛刺信号，需要将$j$对应的分量置为0.然后进行小波反变换，转换为时域信号。

小结

小波分解：

$$f(t) =\sum_{j\in N}\left\lbrace\sum_{i=1}^{j}\psi[2^{i-1}(t-k)]\right\rbrace+\sum_{j\in N}\varphi(t-k)$$

母小波$\varphi(t)$一般具有以下性质：

• 平移正交性：函数自身与平移后的函数相互正交，$\langle \varphi(t),\varphi(t-kT)\rangle =0$；
• 归一化：能量为1，$\langle \varphi(t),\varphi(t) \rangle =\int^{\infty}_{-\infty}\varphi^{2}(t)dt= 1$。

父小波$\psi(t)$一般具有以下性质：

• 平移正交性：函数自身与平移后的函数相互正交，$\langle \psi(t),\psi(t-kT)\rangle =0$；
• 归一化：能量为1，$\langle \psi(t),\psi(t) \rangle =\int^{\infty}_{-\infty}\psi^{2}(t)dt= 1$。
• 与母小波$\varphi(t)$正交。

留个问题：父小波是不是可以和母小波互换呢?

接下来你可能想看： 小波变换(三): 从实例代码看Haar小波分解和重构

参考内容

1. 形象易懂讲解算法I-小波变换
2. 《The Wavelet Tutorial》小波教程 中文翻译（上）
3. python实现小波变换的一个简单例子
4. 小波变换和motion信号处理（一）
5. 小波变换和motion信号处理：第二篇